The hecking fuck, nothing's working. What arcane combination of symbols must I arrange to make media queries work on my phone. Sometime it works, but not actually. The documentation and articles made it sound easy, but the sample codes doesn't even work. Then again, maybe it's just my phone's outdated browser.
I give up, doing calculus suddenly seemed way more easier when trying to make mobile responsive frontend.
There, fixed bugs, and looking good. I want to finish on working on the mobile view so I could test it in the phone before the week ends.
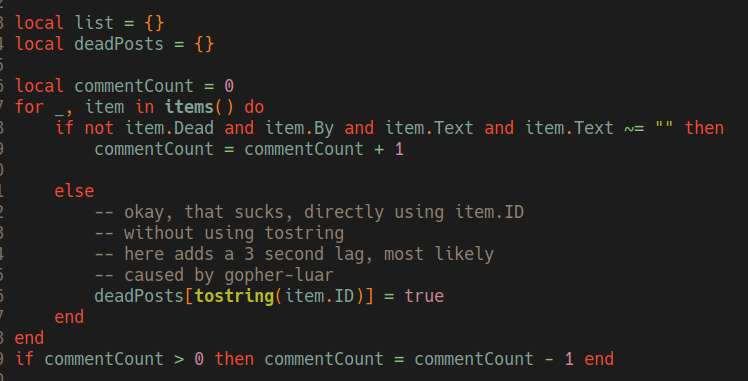
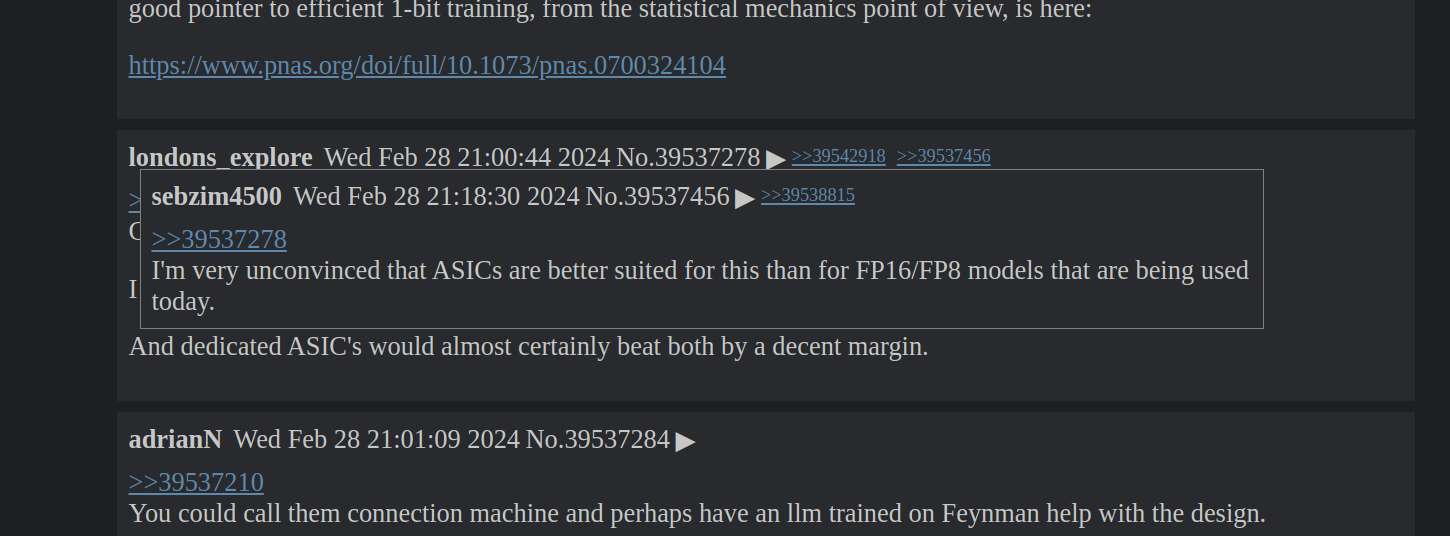
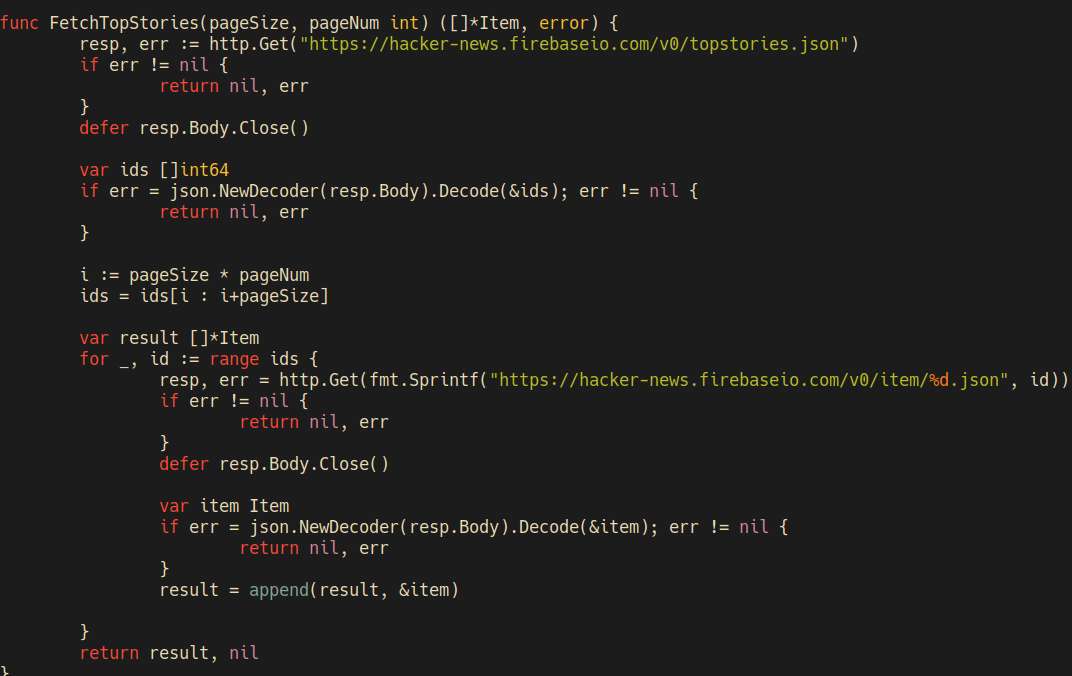
Worked on SN, I fixed several bugs. I also found out that using a field mapped by gopher-luar as a table key causes several seconds of lag. I'm not really why is that, but it's a massive wtf. The fix is to cast the ID first to string before using it as an index.
Also another blocker is the mouseover event. It seems that just moving my mouse inside an element causes the mouseout to emit repeatedly.
Aha, nevermind, fixed it. The bug seems to happen when I nest small elem inside a link: | <a><small>...</small></a> Removing the small fixes the bug. Once again, not sure why would that be a bug in the first place.
Oh well, this is one buggy friday.
So the book did actually and directly used product and power rule for the quotient rule. The approach I did was to start with y = uv~ and get the derivative. But then I wondered, what variable is ∆u and ∆v dependent on? The book used the following notation:
| y = uv | y + ∆y = (u + ∆u)(v + ∆v)
If I let u = w~, how would that affect ∆u? Will it be ∆u~?
Once again, I see and hated the implicit handwavy notations that mathematicians use. I tried explicity converting dependent variables to functions, but then I didn't do any better, it's actually more verbose:
let Y(x) = U(x)V(x)
let ∆Y(x, ∆x) = U(x + ∆x)V(x + ∆x) - U(x)V(x)
= [U(x) + U(∆x)][V(x) + V(∆x)] - U(x)V(x)
= (u + ∆u)(v + ∆v) - uv
where
u = U(x)
v = V(x)
∆u = U(∆x)
∆v = V(∆x)
let Y(x) = U(x)V(x)~
let ∆Y(x) = (u + ∆u)(v~ + ∆v~) - uv~Argh, it's really quite difficult for me when it comes to mobile responsiveness. Things like making sure the text size is right, and all the words and spaces wrap properly. I should properly learn how to do this the right way.
For now, it works enough for me on the desktop. Not on the phone though, it's barely useable with a tiny screen.
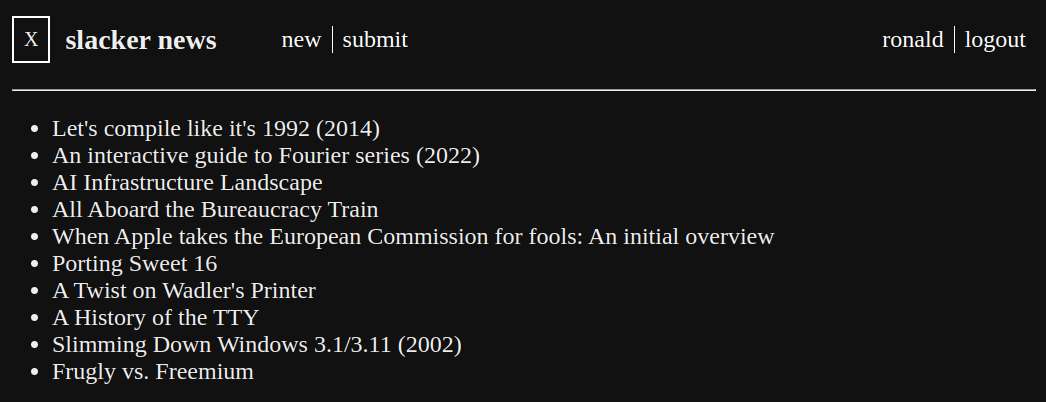
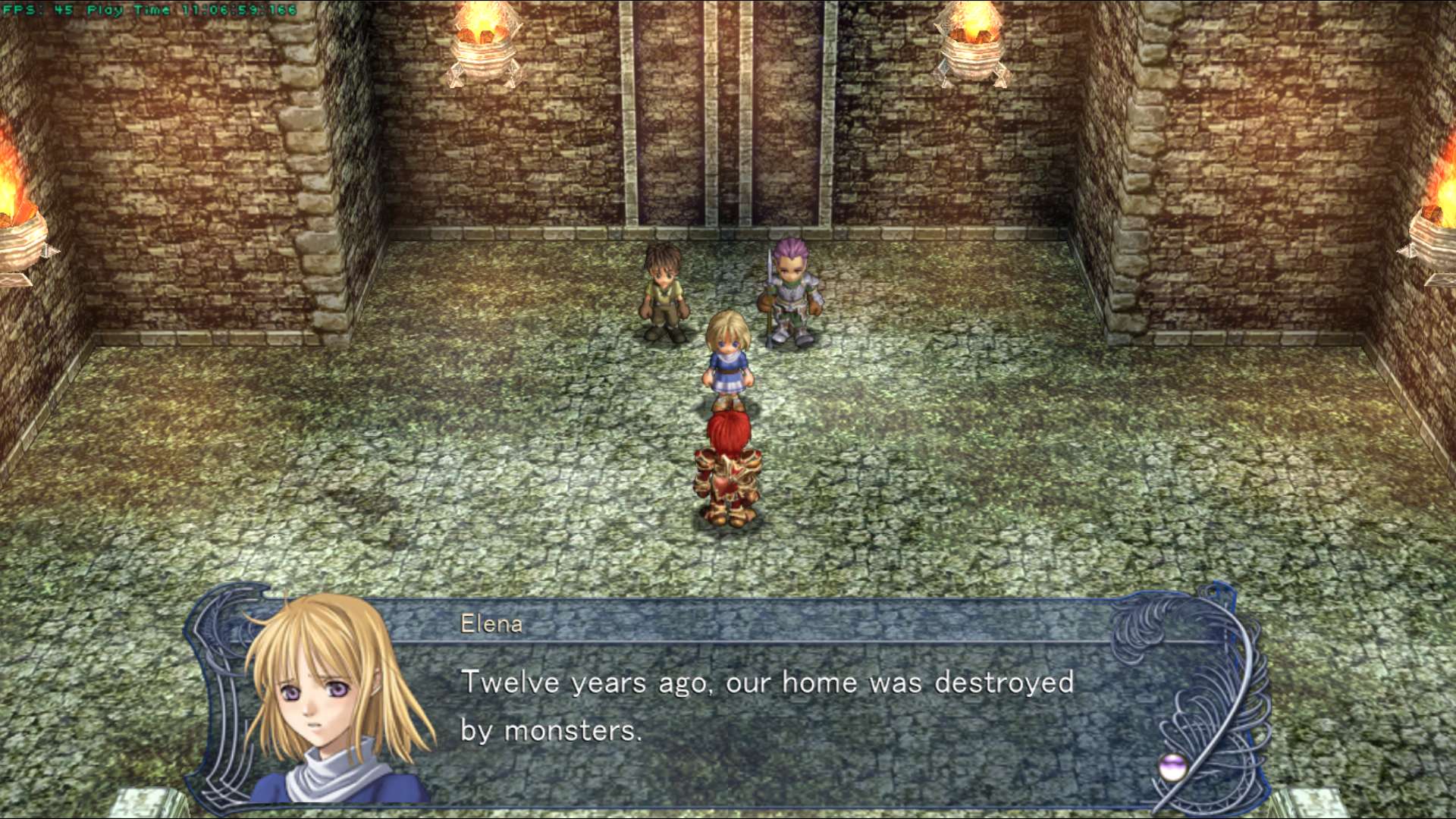
Aha, I managed to almost copy the exact popup behaviour of 4chan. Well, almost, then I saw literal some edge case that needs fixing. Oh well, but for the most part, it's looking pretty good. I might actually use this custom HN frontend from now on.
I unproductively tried to imitate the post popup on hover feature on 4chan. The popup works fine, except the positioning is quite tricky to get it right.
Well, it's supposed to be covered by power rule and the product rule, but I'll check tomorrow. Anyways, I found stuffs on HN that could also fun to learn: geometric algebra.
This tutorial seems to be readable for me https://mattferraro.dev/posts/geometric-algebra only highschool algebra is required.
I'm getting too distracted again though, the last thing I want to surfacely jump from one subject to another without actually ever learning anything. I wonder at what point I will stop reading the calculus book I'm reading right now. It's actually almost a thousand pages long. I could probably stop right until integral calculus, then maybe come to it later in the future.
I'm still reading the book "calculus: an infinitesimal approach". I'm on page 60, and briefly went over the rules for deriving rational functions. Nothing surprising so far, I can still follow along without problem. I should probably frequently go back to these pages and commit these rules into memory.
My eye twitched a bit on the quotient rule though. Isn't division just multiplication with inverses (a/b = ab^-1)? So there shouldn't be a special rule for this, it's covered by the power rule, right?
I'll check just to be sure.
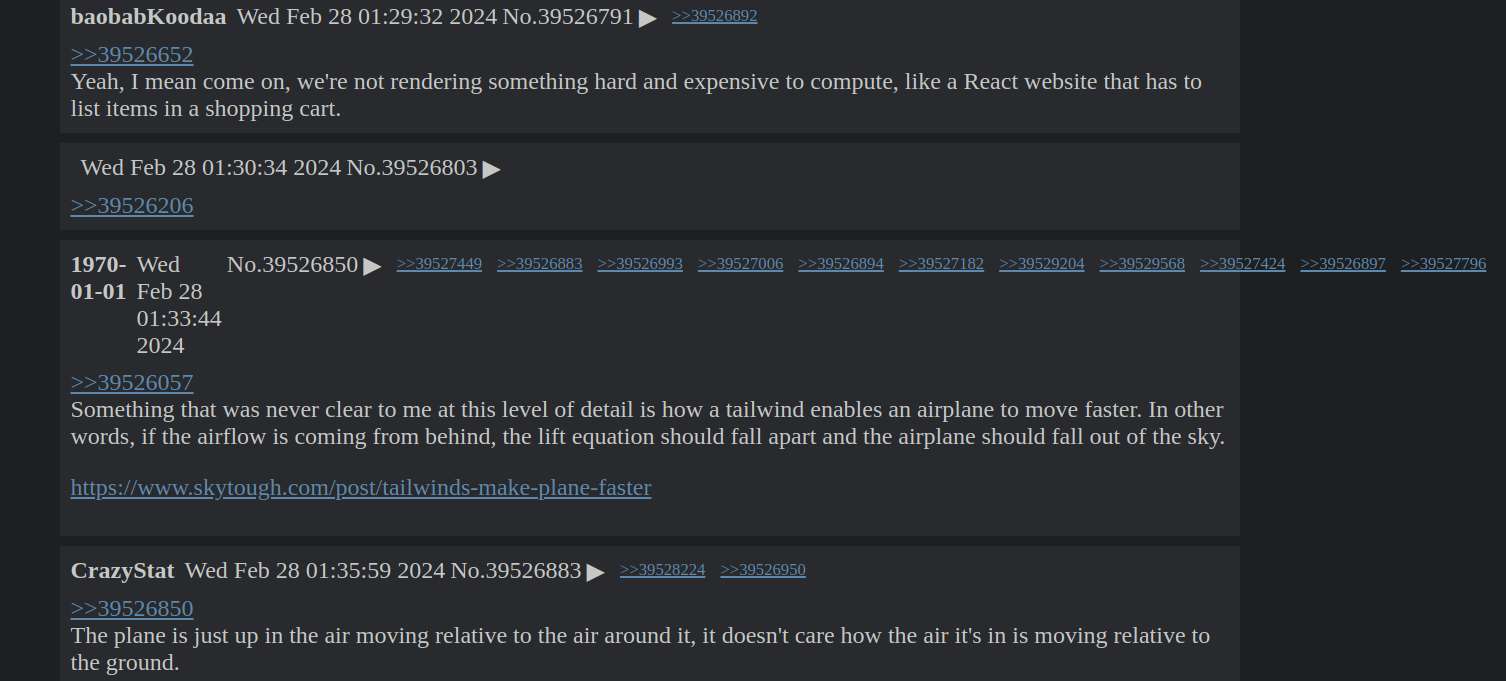
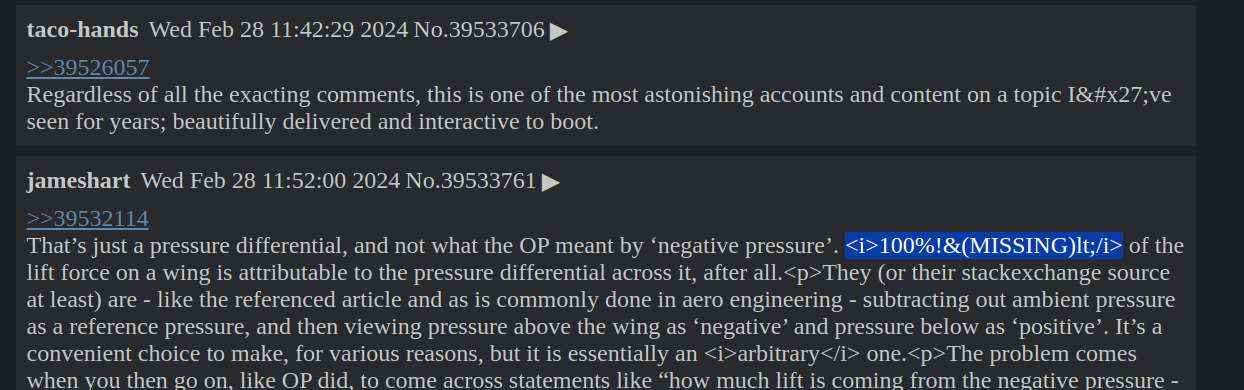
Urgh, I can't believe I spent almost an hour finding out what's causing the
<i>100%!&(MISSING)lt;/i>
bug. I though encoding/json was escaping %, but no. I thought gopher-lua was doing some weird string escaping, no again. I thought gopher-luar was doing some weird string escaping, nope.
Then I thought of printing the text right before writing the response back. Curl was showing the broken text, but the printed text shows the text properly.
Aha, by process of elimination, the source of bug was the code writing the response back:
fmt.Fprintf(w, ret.String())I tried googling for %!&(MISSING) but it shows me an FBI kidnappings and missing person list, lots of kids too. Uh-oh. Damn, look at all the unresolved cases, some dating back all the way to 2010.
I'm reminded that the world is a scary place, you'll never know what sick fuck is lurking around the corner.
Still mostly worked on making the UI look like *chan forum. I found a bug where some tags wouldn't close and end up like `<i>100%!&(MISSING)lt;/i>`. It doesn't happen with direct curl to HN API, so the problem is most likely my escaping function, or the json parser.
Did some "studying" on my rocketbook with calculus notations. I tried writing it in a lua notation so it would be clear what scope each variable is, and are the dependent variables.
One thing I did realize is that Δx is not locally scoped inside the derivative, and that ε isn't really an independent variable as the book suggests.
So once I again, I will try to start from scratch, and write all the functions and equations:
let ∆x be any infinitesimal
let dx = ∆x
let f: func(x: *R)
let derivative = f => x => st{ [f(x + ∆x) - f(x)]∆x~ }
let differential = f => x => derivative(f)(x) * dx
let x be any infinitesimal
let y = f(x)
let slope = derivative(f)(x)
let dy = differential(f)(x)I found an HN post linking to a page of cool stuffs that applies math with programming. In particular, there's Differential equations and calculus from scratch which is highly relevant to what I'm doing.
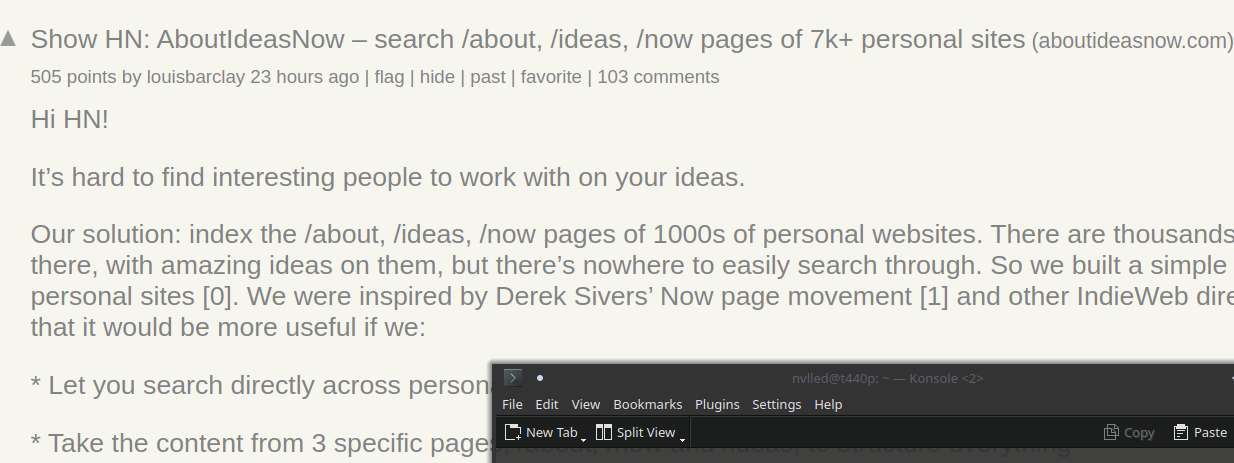
https://news.ycombinator.com/item?id=39511714 I should add some /now on my shitty personal site as well. Not sure about /ideas though, I sure don't have shortage of them, but they are mostly dumb or uninteresting.
I've been wondering too if I should submit my site to aboutideasnow.com, kagi or marginalia. I don't really have any interesting content though. Maybe some time in the future.
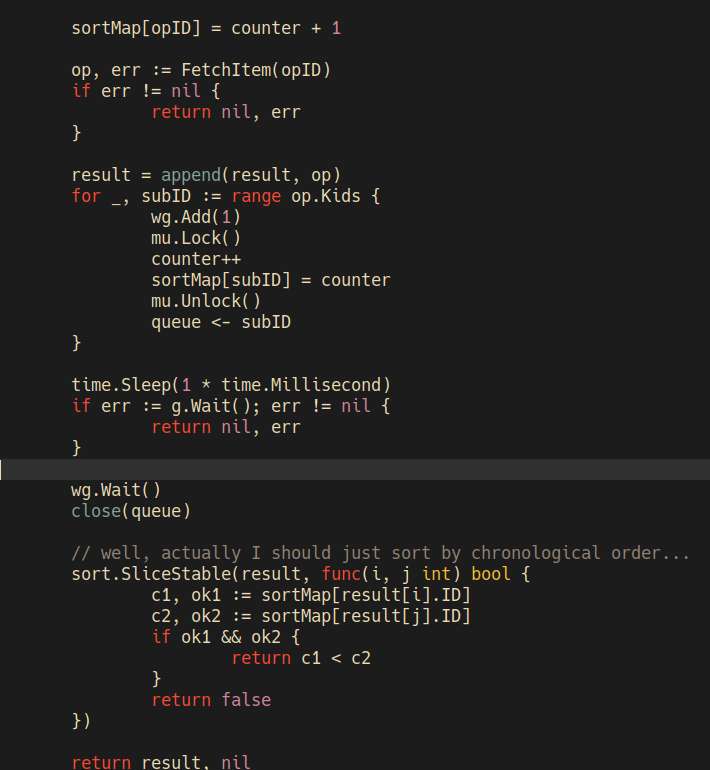
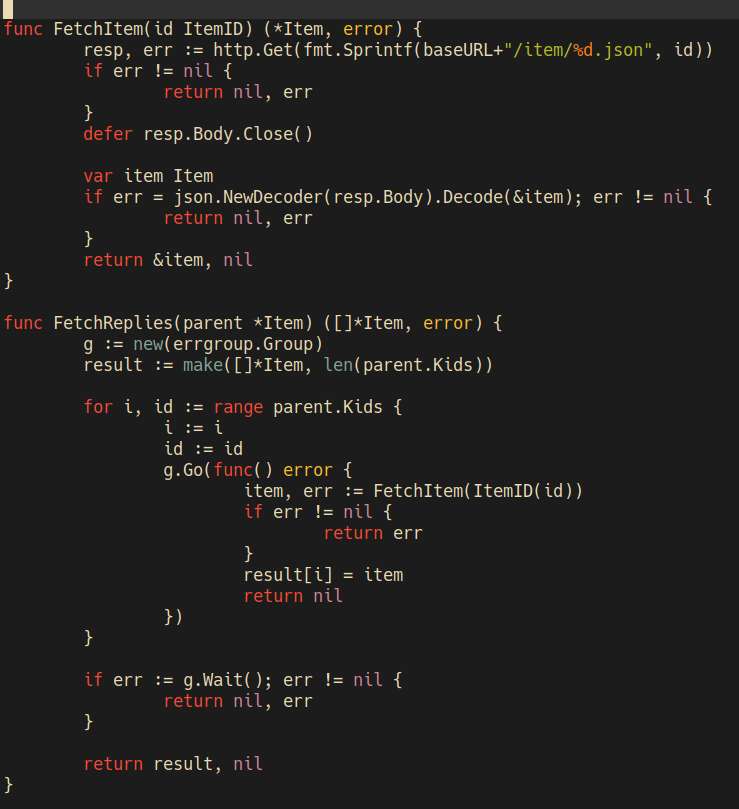
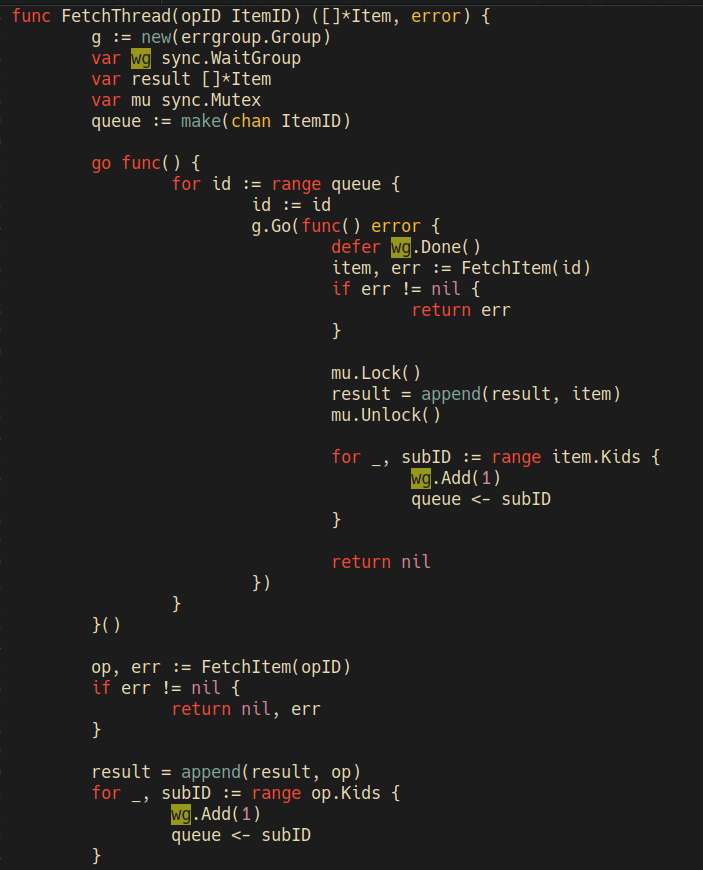
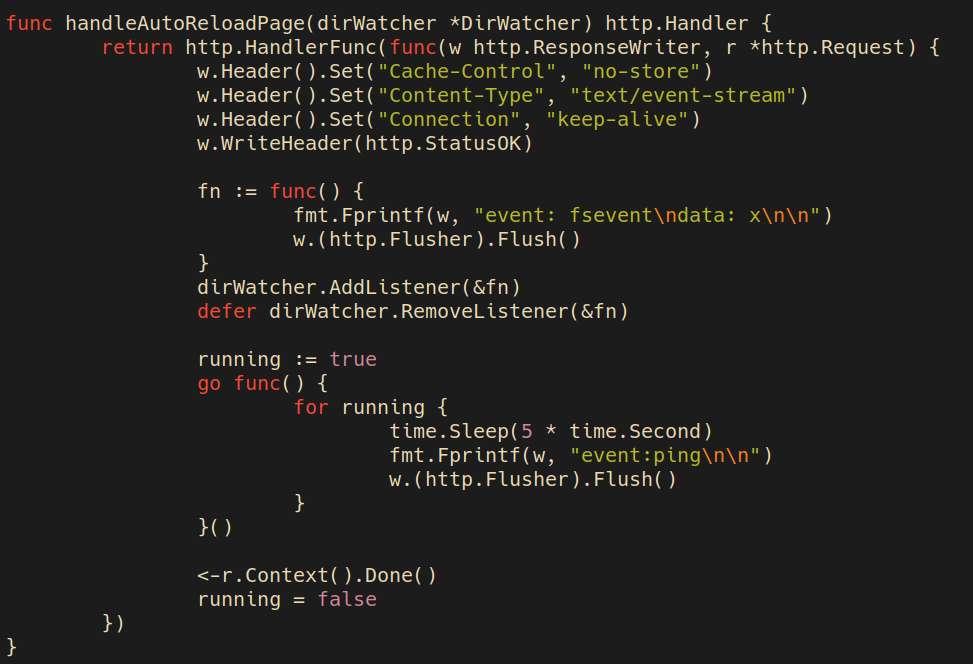
So I noticed that the posts have non-deterministing sorting. I thought, fuck concurrency, I'll just do it without any goroutines, it'll be one http request at a time.
I tried rewriting it, and the code certainly looked simpler. But, it's so, slow. The heck, I thought it would only be a little bit slower, but no, it's about ten times slower on some HN threads.
I undid the rewrite, and just used a map to sort posts by insert order.
Seeing my changes also takes a couple of seconds, so I added some caching to filesystem too, to prevent execessive requests while testing.
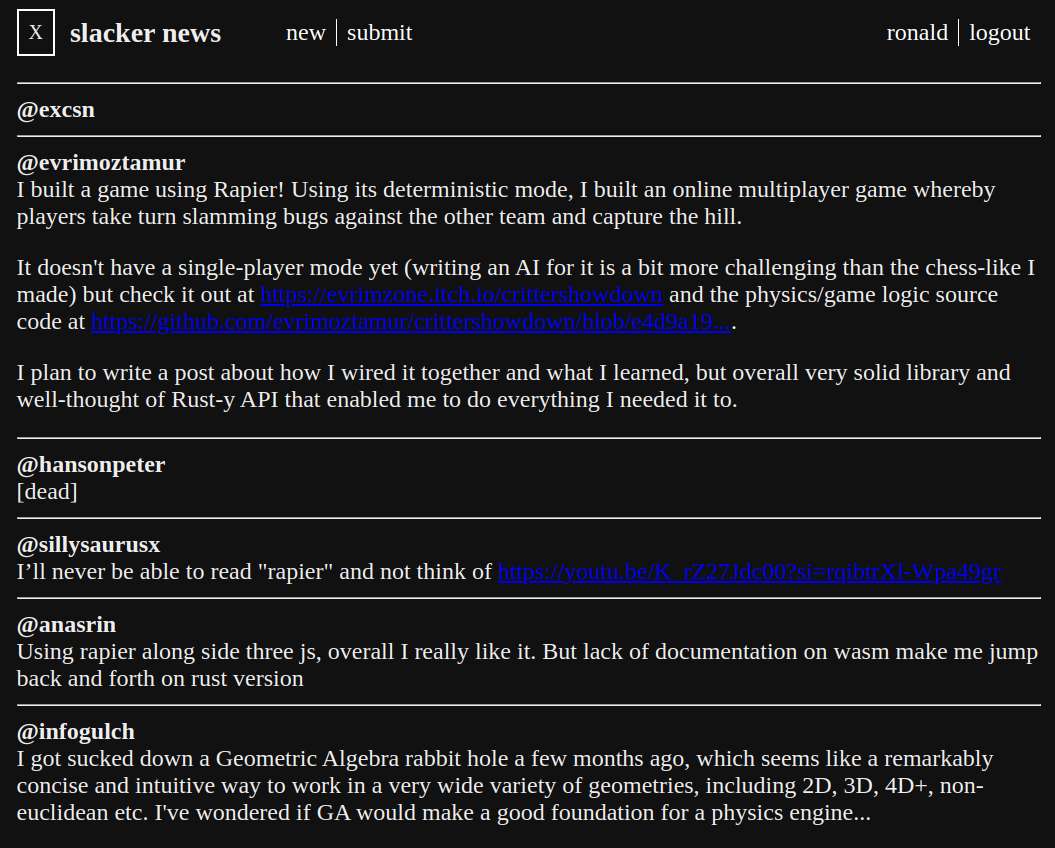
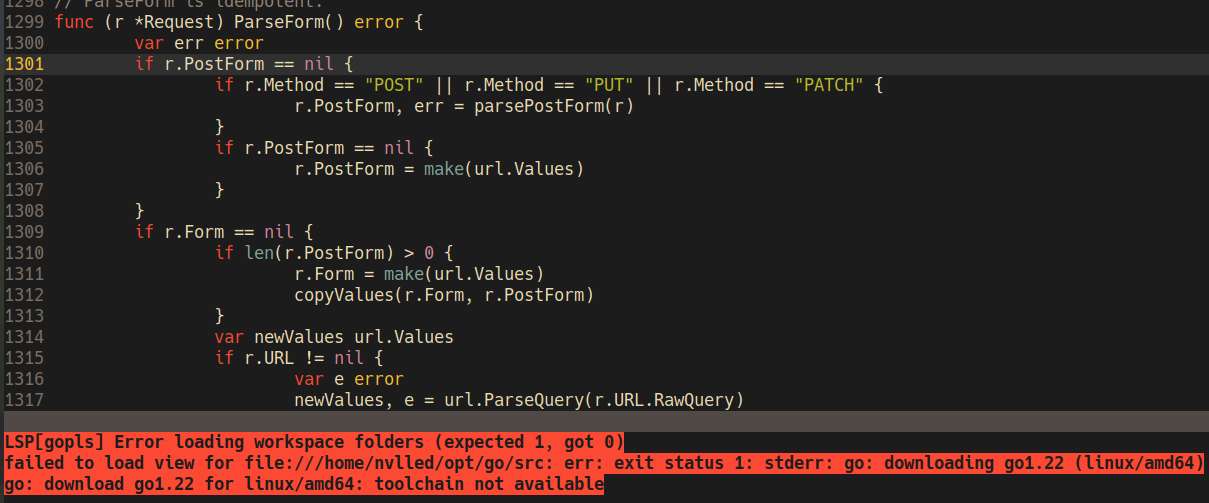
I more or less now have a working basic HN frontend. I think I'll make the UI linear like lainchan/4chan, instead of the usual tree view like reddit and HN. Neovim's lspconfig with gopls is giving me some error though, pretty annoying, not even sure how to fix this.
Wrote some code to handle concurrent http requests. It's never easy to write multi-threaded code, as I'm never sure if there's no deadlock lurking somewhere, or some unexpected race condition will happen. For now, it's working as expected, and it "looks" correct.
I reviewed the notations for derivatives and differentials. I understand it now, but somehow I don't feel all too comfortable with it, maybe it's the concept or the notation. Perhaps I could think of an alternative notation for expressing differentials and derivatives, preferrably something close to a programming language syntax.
Next time I'll be reading the rules for differentiating rational terms. These rules are what are usually taught in schools to be rote memorized I think.
I decided to use the official HN api while creating the frontend first. That way, it's easier to create a compatible backend later on.
Aha, I think I understand now. ∆y/∆x ≈ f'(x) does actually makes sense. I had an imprecise definition of derivative in my head. More precisely, the derivative f'(x) is
f'(x) = st(∆y/∆x)
f'(x) - (∆y/∆x)
= st(∆y/∆x) - ∆y/∆x
= ε
∆y/∆x ≈ f'(x)
∆y/∆x - f'(x) = ε // by definition of infinitesimal
∆y/∆x = f'(x) + ε
∆y = f'(x)∆x + ε∆xI did consider and downloaded other books about infinitesimal calculus, but I didn't find any mention of the increment theorem. It would probably be better if I skim through at least one of them, to further solidify my understanding. In the end the wikipedia page was enough to clear up my understanding. Or maybe, a weekend break, consisting of turning my brain off.
I'll spend more time getting used to the notation shown on page 56, and I'll need to have a very intuitive understanding of increment theorem, because it seems important to gloss over.
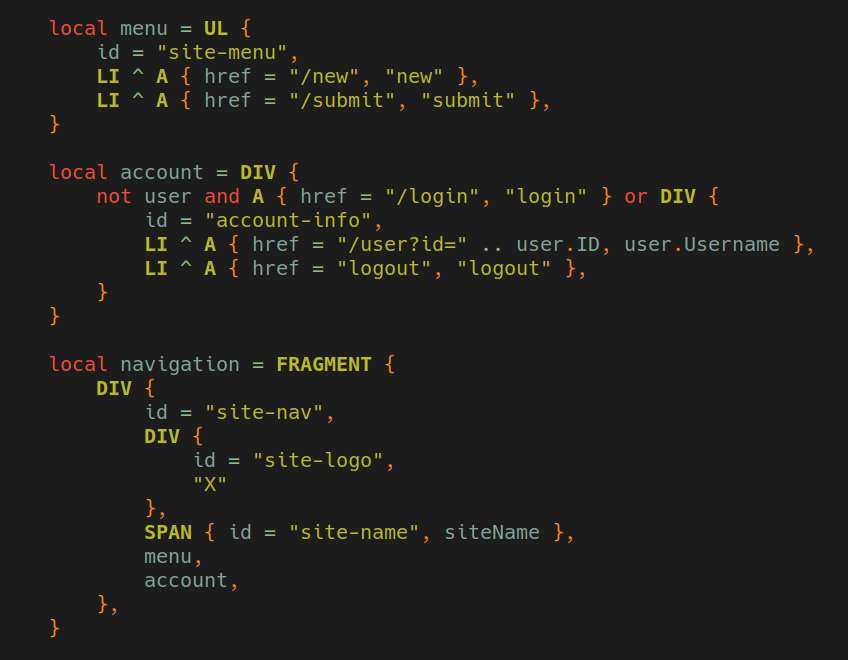
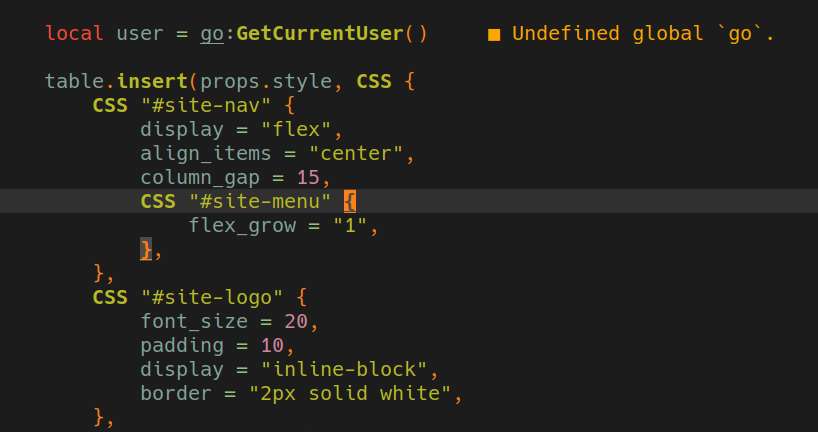
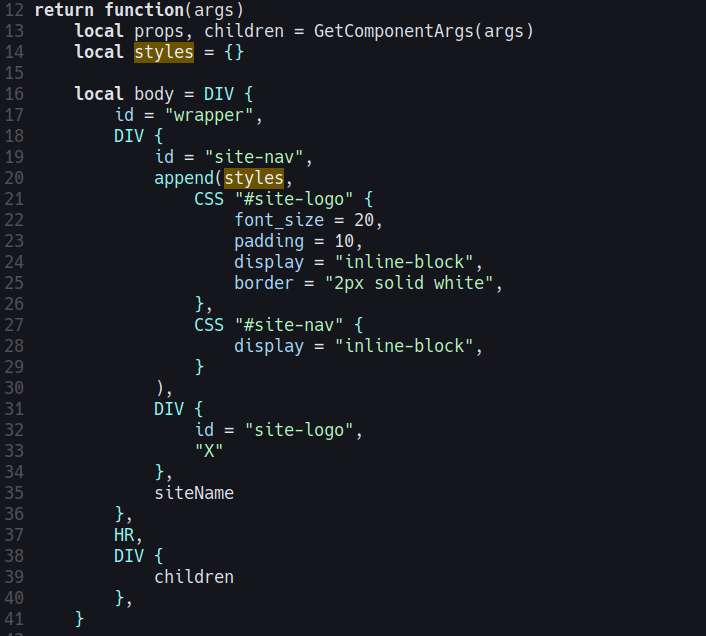
Worked on the website using the lua templating. On my filesystem, I tentatively named the project folder as goom-temple, which actually sounds inappropriate since goom jokingly refers something specific for a certain shark fanbase, but it doesn't matter, it's just a temporary name. For brevity, I'll refer to this project as SN (slacker news) for now.
As expected, I haven't done much for today, most of which are scaffolding stuffs for the overall project structure. I also properly configured my neovim lsp this time, both for lua and go.
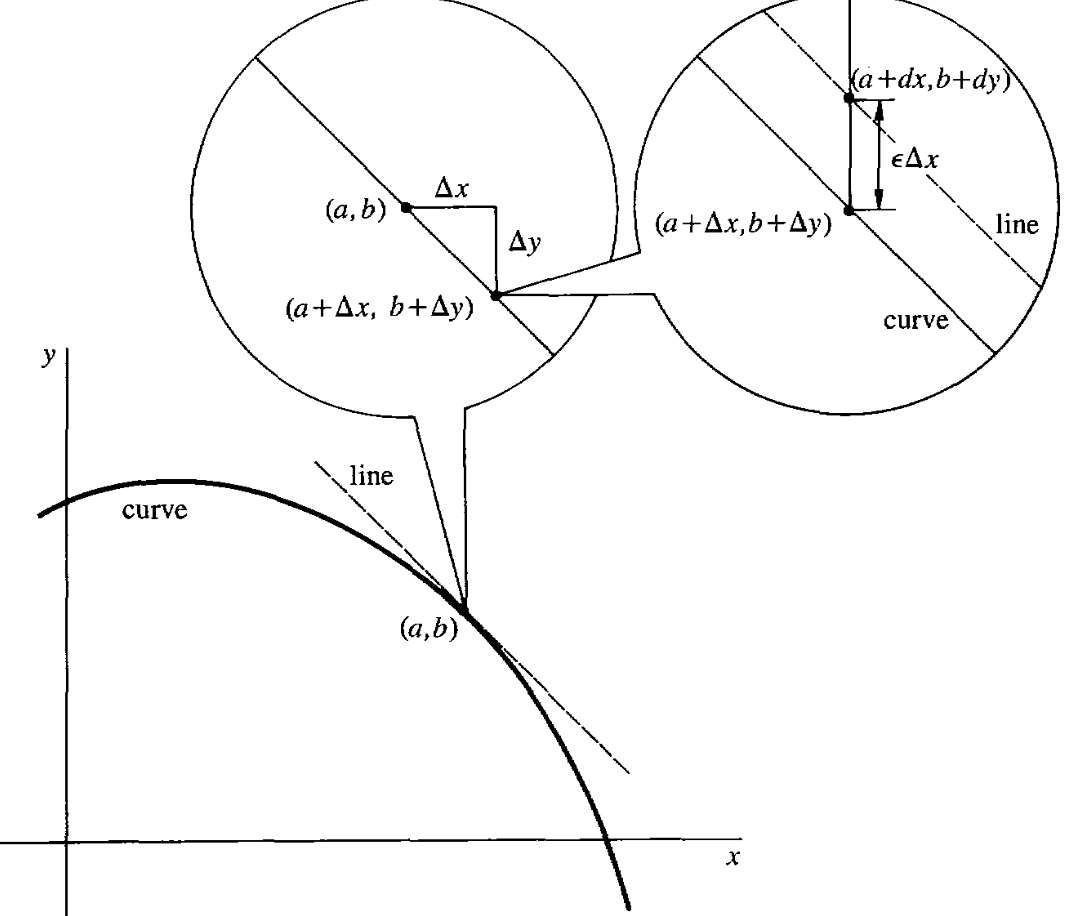
Okay, I think I am infinitely close to understanding what the heck increment theorem is supposed to mean.
- I have a shitty curve f(x)
- derivative of f(x) is f'(x), which just maps x to a slope
- I can use the slope f'(x) to create a straight ass linear curve l(x)
Then at point [x, f(x)] and another point [x+∆x, f(x+∆x)] The change in y (f(x+∆x) - f(x)) along the f(x) is called "increment of y"?, notated as ∆y The change in y (l(x+∆x) - l(x)) along the l(x) is called "differential of y, notated as dy
The increment theorem says that the distance between ∆y and dy is εΔx, not that it helps why that matters.
Then somewhere in the book says that
∆y/∆x ≈ f'(x) (squiggly equal lines) and
dy/dx = f'(x)Well technically, any number x ≈ x since x-x = 0 + ε, so it could be that both ∆y/∆x ≈ f'(x) and ∆y/∆x = f'(x) is true.
Oh well, I may need to consult an alternative resource for a different explanation. At least for the increment theorem. I understood well what derivative and differential means. I should probably reviews the definitions for infinitesimal as well.
I wiped my most of my rocketbook pages, so I could have more space for weird symbols to scribble on.
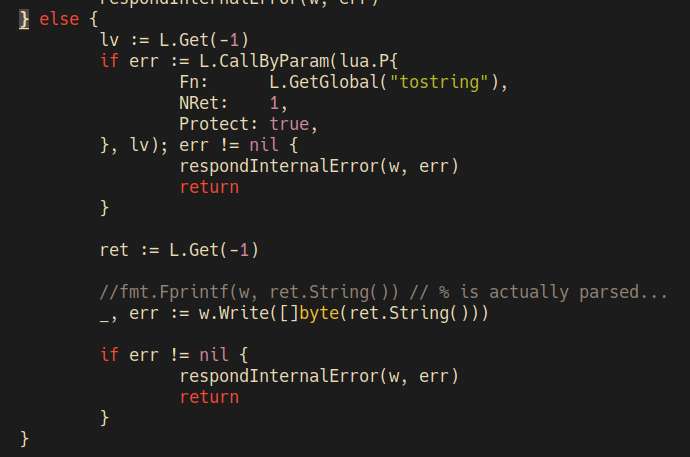
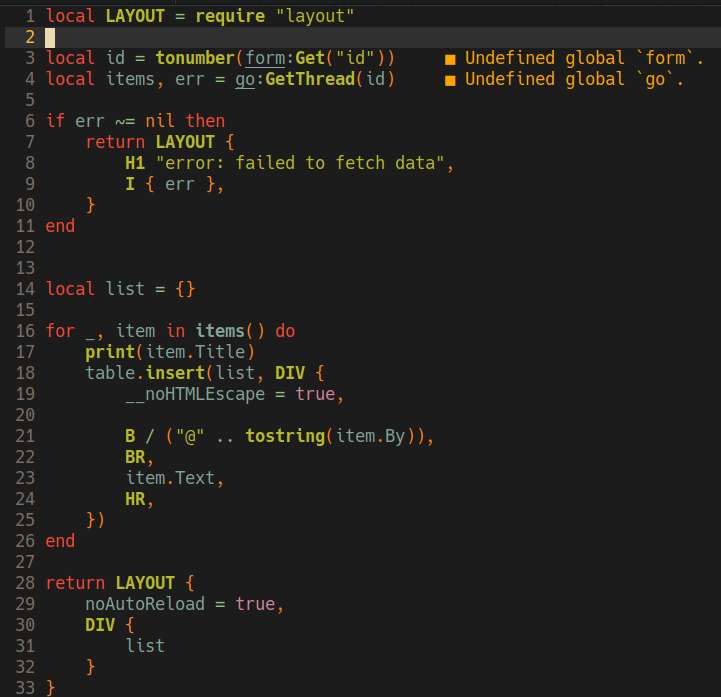
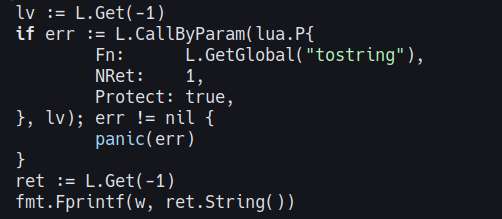
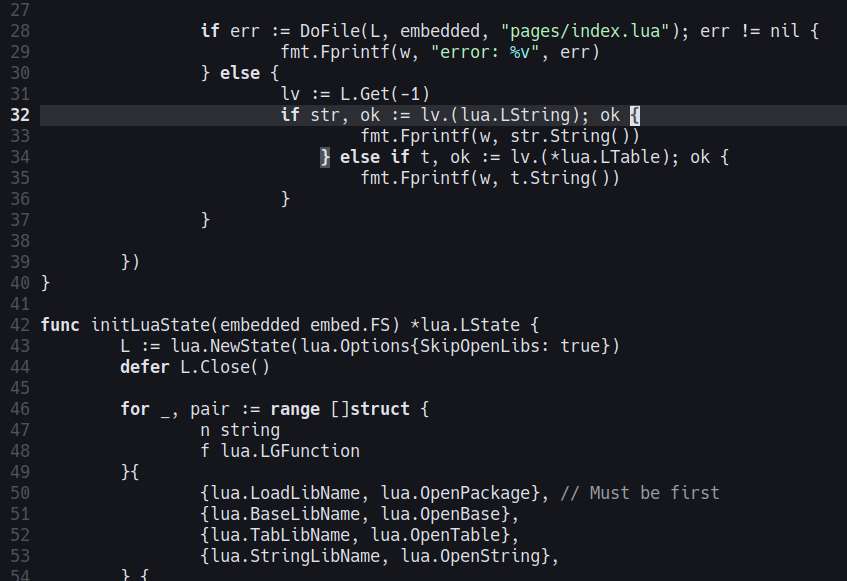
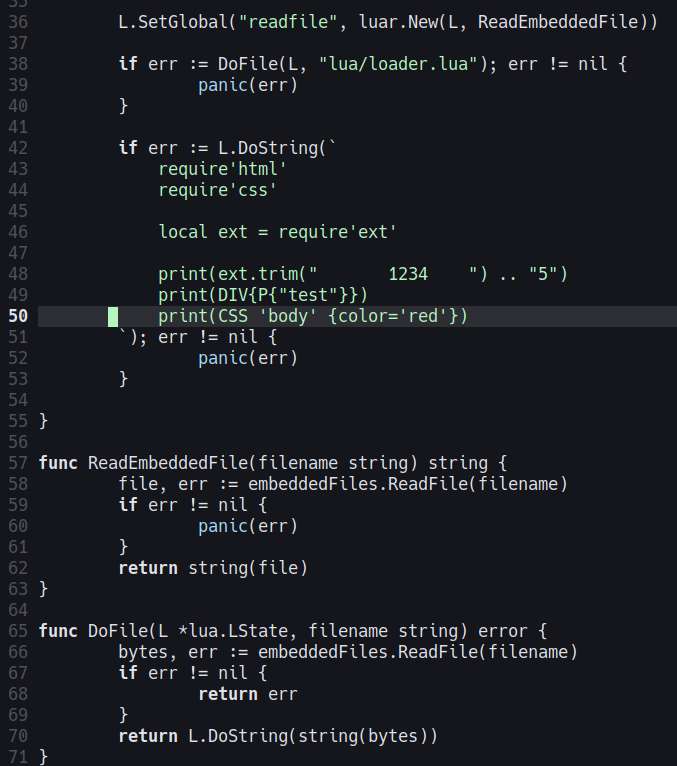
There fixed the __tostring problem by using L.CallByParam. I also had to create my own version of dofile since the one provided by gopher-lua doesn't allow setting the chunk name, and seeing chunk name is important when debugging.
I considered using htmz, but since hacker news doesn't have a lot of UI interactivity, it's not needed for this toy project.
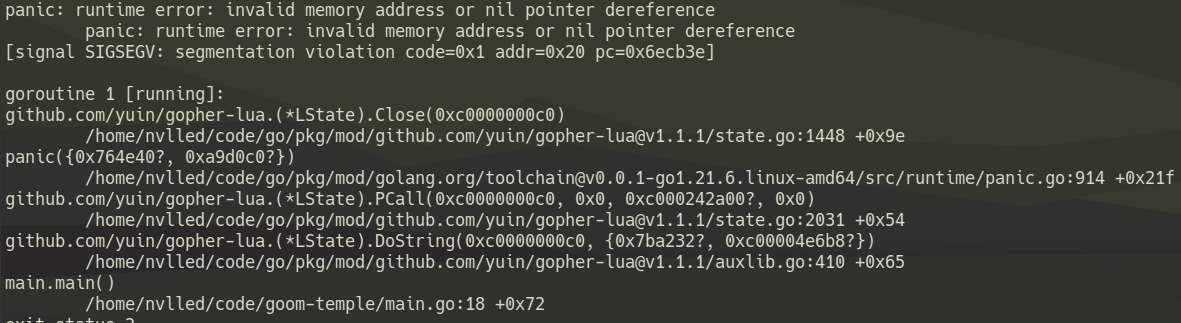
I was wondering why I keep getting a nil pointer dereference, as it turns out, I'm closing L.close() before I could even use L. Now my problem is why the __tostring metamethod isn't being called from the go code. I'm currently looking for code examples how to do that, or just examples how to better use the gopher-lua API.
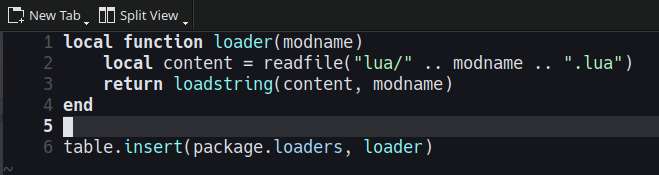
Worked on getting the lua environment to work with gopher-lua. The custom loader solution works fine, now I just to figure out a way to structure the web application. For demostration purposes, I'll just create a simple HN clone.
Oh, I see I what's going on here:
l(x) - b = f'(a)(x - a)
l(x) = f'(a)(x - a) + bWhat I want:
- scoping of variable for each functions
- dependent variables should be clear whose variable it's depending on
- still have the freedom of doing algebraic manipulations (or equational reasoning? as the FP guys say)
lol, I didn't realize my computer crashed, all input was unresponsive, but it was still playing the same tune 3 second tune in a loop. Oddly enough, it still quite catchy, so I didn't notice until I tried moving my mouse.
Anyway, I was on my notebook wondering what the geometric interpretation of negative exponents. n^m makes sense, it just multiplication. But what about n^-m, it's not apparent at first, but it's just equal division. What about n^(m^-1)? n^0.5 is square root, but what does that mean? Isn't that division as well? Maybe unequal division?
As it turns out, I don't really understand the basic, fundamentals of math. But why stop at multiplication and division. Maybe there's a weird arithmetic operator that has useful properties. Base-2 has `xor`, `nand` and other operators.
What if xor and others was generalized to arbitrary base? So instead of bit-wise pairing, on decimal, it would be digit pairing. What properties woud those operator have?
Can I define some weird operators too? Programmers after all do that all the time, well, haskell programmers do at least.
I will set aside these thoughts for now, I have a calculus book to read.